【ガチ計算】「オニゴーリ」の回避率上昇確率の検証

ページを開いていただきありがとうございます！世界一どうでもいいポケモンの考察事項ではありますが、魂を込めて結論まで書きあげたのでぜひ最後までお付き合いいただけると嬉しいです。この記事を読むことで、何ターンムラッケの試行回数を与えると自分側が不利になってしまうのか、知ることができます

この記事はかなーり理系ほいほいな記事になっております。しかし数学があまり好きではないという方でも、結論は共有できるように工夫したつもりです。ですから適宜飛ばし読みしながらお好みでお楽しみください。

§1．前書き～日々運負けをくらう皆さんへ

ポケモントレーナーの皆様、日々のレーティングバトルの業務お疲れ様です。岩石封じをはずした…メタグロスに連続でひるまされて負けた…などなど理不尽な負けに堪えがたき日々を過ごしていらっしゃると思います。その中でも特に不条理な、受け入れがたい現実をおしつけてくるのがポケモン界のアイドル“オニゴーリ”であり、不意に自らの回避率を上昇させトレーナーたちを絶望へと誘います。

「ちゃんとゴーリの起点にならねぇように初手からゴーリより早く十分な削りができるやつ出したのに、1ターン目に回避上げられ、次攻撃外してみがまもの起点にされて零度あてられた。マジでこのゲームクソゲー過ぎんか？(# ﾟДﾟ)一生やらんわｗはい引退！ｗ」

ツイッターに寄せられるこのような阿鼻叫喚を極めし声は枚挙にいとまがなく、見るたびに同情の目を向けせざるを得ません。このような体験をし、一時はあんなにも必死に頭を悩ませ時間を費やしたポケモンというゲームから退いてしまうプレイヤーも多いのではないでしょうか。

私自身も過去にそのような現実に直面してから長らくポケモンはカジュアルに、第三者的な視点で楽しんでいたのですが、ひょんなことから最近レーティングバトルに復帰しました。やはりゴーリと「対面」することにはなってしまったのですが、案の定その試合では数ターンで回避の舞をくらい早々に試合を決定づけられてしまいました。目の前に起こった現実をどうしても消化することができず、これほどの不運、果たしてどれほどの確率で起こりうるものなのか実際に自分の手で確かめることで自分を慰めることにしました。せっかくですのでその考察の過程と結論を皆様と共有できたらなと思い僭越ながら筆を執る次第となりました。

§2．ムラッケについて

ムラッケ発動時に回避率が二段階上昇する確率 $\frac{1}7$

同時にムラッケ発動時に回避率が一段階落ちる確率 $\frac{1}7$

HPマックスの状態からまもみがは16ターン繰り返すことができる

それゆえにツイッターでは「16ターン連続で少なくとも一度回避率が上がる確率は1- ${(\frac{6}{7})}^{16}$ ≒92％だから云々」というツイートが散見されますが冷静に考えればもう少し低いはずです。なぜなら回避率は上がるだけでなく下がる可能性もあるからです。今回はその回避率が下がるという事象も加味してより正確に確率計算をしていこうと思います。

とはいえポケモンのランクは＋６から－6まで13段階あり、ゴーリ側がまもみがを開始してからｎターン後におけるランク上昇をすべて追うのは困難を極めます。そこで簡単のために、高校数学でも十分解析可能な以下のような条件を付したモデルで議論していきます。（多分すべてのランクを追うには大学レベルの難しい数学が必要(+_+)）

§3．計算過程

以下のような3つの設定で議論します。

回避率が2段階上昇、1段階下降する確率はそれぞれ $\frac{1}7$
回避率は一度上昇したらそれ以降落ちることはない
3回避率が－２ランクにまで落ちたらそれ以降回避率が上昇することはない

以下の議論は高校で数学Bを履修していないと理解不能だと思われるので未修の方は§４の結論部まで飛ばしてください。目標は、「ｎターン目までに回避率が上昇する確率の一般項 $s_n$ を確率漸化式によって導出し、 $S_n$ ＞ $\frac{1}{2}$ を満たす最小の自然数ｎを特定する」ことです。実際に議論を進めてみたところ、実際に出題されてもおかしくないちょうどよい難易度の数列の入試問題が出来上がってしまっていたので、理系の特に受験生の方や大学生になってしまったけど東大も捨てがたい方はぜひ自力でチャレンジしてみてください。（数学の問題って楽しいよね←）

問題　以上３条件で

ｎターン目に回避ランクが±０である確率 $a_n$ を求めよ
ｎターン目に回避ランクが－1である確率 $b_n$ を求めよ
ｎターン目までに回避率が上昇する確率 $s_n$ を求めよ

答え

　状態を図示すると以下のようになります。（パソコン初心者で不慣れでごめんなさい(._.)）

f:id:hanamiti19:20190101093335p:plain — 最新

　図3.1みがまも０ターン目と１ターン目の遷移図

f:id:hanamiti19:20181226210017p:plain

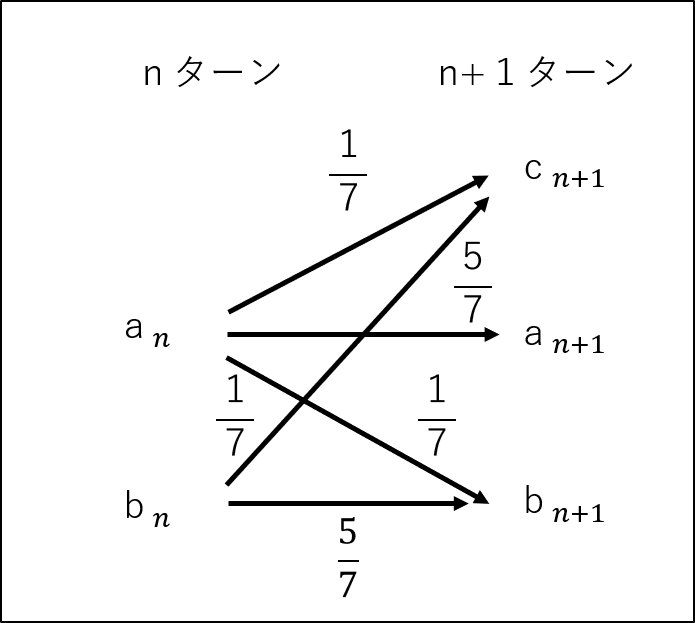
　図3.2みがまもｎターン目とｎ＋１ターン目の遷移図

上図より以下のような漸化式が成立します（なんか唐突に始まりやがった）

$a_{n+1}＝\frac{5}7a_n$ 　　　　（3.1）
$b_{n+1}＝\frac{1}7a_n+\frac{5}7b_n$ 　　　（3.2）
$c_{n+1}＝\frac{1}7(a_n+b_n)$ 　　　（3.3）

まず式（3.1）は等比型の基本的な漸化式であり初項は

$a_1＝\frac{5}{7}$ 　　　　（3.4）

であるからこの漸化式を解くと

　 $a_n＝{(\frac{5}{7})}^{n}$ 　 (3.5)　　問題(1)の解答

となります。(3.5)式を(3.2)式に代入すると

$b_{n+1}＝\frac{1}{7}{(\frac{5}{7})}^{n}+\frac{5}7b_n$ 　(3.6)

となります。この $b_n$ に関する漸化式の両辺を ${(\frac{5}{7})}^{n+1}$ で割り、新たに $d_n$ を式(3.7)のように定義することで（3.6）の漸化式を等差型の漸化式(3.8)にすることができます

$d_n＝\frac{b_n}{{(\frac{5}{7})}^{n}}$ 　(3.7)
$d_{n+1}＝d_n+\frac{1}5$ 　(3.8)

ところで $b_n$ の初項は

$b_1=\frac{1}{7}$ 　　（3.9）

なので（3.7）より $d_n$ の初項は

$d_1=\frac{1}{5}$ 　　（3.10）

となります。式（3.8）および（3.10）より $d_n$ の一般項

$d_n＝\frac{1}{5}n$ 　 (3.11)

を得ます。これより式（3.7）に代入することで $b_n$ の一般項を得ます。

　　　　　　 $b_n=\frac{1}{5}n{(\frac{5}{7})}^{n}$ 　（3.12）　　問題(2)の解答

ってか普通に青チャとかにありがちな特殊な漸化式の問題みたいになってますね（なげえ）

こうして式（3.3）に（3.5）及び（3.12）を代入すると $c_n$ の一般項を得ます。 $c_n＝\frac{1}{7}{{(\frac{5}{7})}^{n-1}+\frac{1}{5}(n-1){(\frac{5}{7})}^{n-1}}＝\frac{1}{25}{(\frac{5}{7})}^{n}(n+4)$ 　　(3.13)

この $c_n$ はｎターン目に回避率が上昇する確率であったのでｎターンまでに回避率が上昇する確率 $S_n$ はこの $c_k$ をk=1からｎまで足し合わせたものになるわけですから、

$S_n=\sum_{k=1}^{n}c_k$

$=\sum_{k=1}^{n}\frac{1}{25}{(\frac{5}{7})}^{k}(k+4)$ 　(3.14)

となります。そしてこのΣ計算をこれ以降一生やっていきます。（まだあるんかい）

とりあえずこのΣ計算を二つに分けて計算する。 $T_n$ を次のように定義する

$T_n=\sum_{k=1}^{n}{(\frac{5}{7})}^{k}$ 　(3.15)

とすればこれは等比数列の和の計算だから

$T_n=\frac{5}{2}-\frac{7}{2}{(\frac{5}{7})}^{n+1}$ (3.16)

また $u_n$ も次のように定義すると

$u_n=\ \sum_{k=1}^{n}{{(\frac{5}{7})}^{k}k}$ 　（3.17）

とすれば、これは等差と等比の積の和であり以下のように等比 $\frac{5}{7}$ を $u_n$ をかけて引くことで計算する(教科書の例題でよくある奴)

$u_n=\frac{5}{7}+({\frac{5}{7})}^2\times2+\ldots+({\frac{5}{7})}^n\times n$ 　(3.18) $\frac{5}{7}u_n= ({\frac{5}{7})}^2\times1+\ldots+({\frac{5}{7})}^{n}\times (n-1)+({\frac{5}{7})}^{n+1}×n$ 　(3.19)

(3.18)から（3.19）を引くと

$\frac{2}{7}u_n={\frac{5}{7}+({\frac{5}{7})}^2+\ldots+({\frac{5}{7})}^n}-({\frac{5}{7})}^{n+1}×(n+1)$ $＝T_n-({\frac{5}{7})}^{n+1}×(n+1)$ 　（3.20）

（3.16）及び（3.20）を整理して用いて（3.14）を計算すると（急に雑になる奴）

$S_n=\frac{3}{4}－\frac{1}{20}({\frac{5}{7})}^{n}（2n＋15）$ （3.21）　問題（3）の答え

となります。これでやっと「ｎターン目までに回避率が上昇する確率」を求めることができました。（検算は何回かしたけど間違っていたら指摘してください。ってかまじめにもう読んでる奴いないでしょうね笑）

飛ばし読みした人はここで戻ってきてください

4．結果と考察

さてやっと具体的な値の計算ができますね（ぐったり）。改めて、「ｎターン目までに回避率が上昇する確率」は上記（3.21）により計算できます。

$S_n=\frac{3}{4}－\frac{1}{20}({\frac{5}{7})}^{n}（2n＋15）$ 　（3.21）

（ｎにあるターン数を入れることでそのターンまでに回避率が上がる確率を計算できるということです）

まもみがにより１６回の試行回数得たゴーリ側は（ｎ＝16を代入すると）

$S_{16}$ ≒74％　の確率で回避を上げることができます。最初に提示した92％よりかは小さくなって良い正確な値に近づいていると思われます。。

また $S_n$ ＞ $\frac{1}{2}$ 　を満たす最小の自然数ｎは　（ $S_n$ の単調増加性は自明ということで）

$S_4$ ＝45％　
$S_5$ ＝52％

となるので、５回ムラッケの試行回数を与えてしまうといわゆる確率的に不利な「文句が言えない側」になってしまいます。いかにムラッケの試行回数を与えないプレイングをすることが大事なことであるかわかる数値といえますね。逆にこの数値が分かっていれば、試合中に「これだけムラッケの試行回数を与えてしまったのだからしょうがない」とあきらめがつくようになるかもしれません

ちなみに回避率の上昇確率と銘打ったのですがもちろん素早さなど他のパラメータにも適用できます。

（補足）　このモデルにおける精度に関する評価（読み飛ばし推奨）

１ターンのランク変化の期待値は（＋2）× $\frac{1}{7}$ ＋（－1）× $\frac{1}{7}＝\frac{1}{7}$ ＞０　と正の値となっており、少なくとも十分時間がたてばランクは必ず上昇するはずですから{tex:S_n→1]と収束するはずです。しかし（3.21）式においてｎ→∞とすると $S_n→\frac{3}{4}$ 　となってしまい１ではない値を取ってしまっています。これはこの簡易モデルが引き起こしてしまっている問題点であり限界点でもあります。 $\frac{3}{4}$ に収束していることからこのモデルの精度は75%といえるでしょう(適当)

5．あとがき

完全に理系オタク丸出しの暇人記事になってしまいましたが、ここまでガチでゴーリの回避率上昇計算をしたことのあるトレーナーも少ないのではないでしょうか。こういう楽しみ方ができるのもポケモンのいいところですよね。（特に理系の方々は少しでも楽しんでくれてたらうれしい(^-^)）もしこの記事を読んで、より正確に計算してみたよって人がいればぜひぜひ教えてください！

面白いと感じた人はぜひリツイート、気持ち悪いと思った人は引用リツイートで悪口言いながら拡散しちゃってください！FFじゃない人にもこの記事が届いていろいろと話せればいいですね

ポケモンバトルには確率という要素が非常に大きく絡んできます。他に、じゃあこうこうこういうことが起こるのってどのくらいの確率なんだろう…と疑問に思われた方がいたら質問お待ちしております。

次の記事は人生初レート2000達成構築記事を書きたいなあ…

質問、アドバイス、指摘、いちゃもん、挑発などございましたら＠have_poke にてお願いします。

ここまでの拝読感謝いたしますヾ(≧▽≦)ﾉ

（あとHatenaBlogってLaTexで数式書かなきゃいけなくてめっちゃ疲れるね。プログラミングの沼にはまりそうだわ。Wordしか使えなかった雑魚にはすげえこたえましたわ（笑））